§4.3 分部积分法
设函数![]() ,
, ![]() 具有连续导数, 那么
具有连续导数, 那么
![]()
移项得:![]()
对这个等式两边求不定积分,得:
![]() (1)
(1)
式(1)称为分部积分公式。
(1)还可表述成如下形式:
![]() (2)
(2)
它的作用是:
若求![]() 有困难,而求
有困难,而求![]() 较容易时,可采用分部积分公式。分部积分法是数学上常用的一种方法 — 转化法的具体运用。
较容易时,可采用分部积分公式。分部积分法是数学上常用的一种方法 — 转化法的具体运用。
【例1】求 ![]()
解:设![]() ,
, ![]()
![]() ,
, ![]()
![]()
在进行分部积分时,把被积表达式中的哪一部分取作![]() ,
,![]() 是任意的。但是,如果
是任意的。但是,如果![]() 与
与![]() 的选取不恰当,往往使问题变得更复杂。
的选取不恰当,往往使问题变得更复杂。
例如,在上例中,若选择
![]() ,
, ![]()
那么
![]() ,
, ![]()
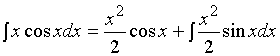
显然,求 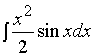 较
较 ![]() 更困难。
更困难。

【例2】求
![]() ,
,
![]()
解:![]() ,
, ![]()
![]() ,
,
![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]()
![]()
所以 ![]()
这表明:可连续使用分部积分法。
【例3】求
![]()
解:设 ![]() ,
, ![]()
![]() ,
, ![]()
![]()
再设 ![]() ,
, ![]()
![]() ,
, ![]()
![]()
![]() (*)
(*)
将![]() 移到左端,两端同除以2,并加上任意常数 C,得到:
移到左端,两端同除以2,并加上任意常数 C,得到:
![]()
例三的评注:
1、求![]() ,使用两次分部积分法得( * )式,又转回到
,使用两次分部积分法得( * )式,又转回到![]() 。表面上看,我们在转圈子,并没有前进,实质上却不然。
。表面上看,我们在转圈子,并没有前进,实质上却不然。
若设![]() ( 是一个未知函数) ,则有
( 是一个未知函数) ,则有
![]()
这是一个关于![]() 的一元一次方程,问题转化为求此方程的解。很明显,我们的确把问题的解决大大地向前推进了一步,并未落入“怪圈”。
的一元一次方程,问题转化为求此方程的解。很明显,我们的确把问题的解决大大地向前推进了一步,并未落入“怪圈”。
2、怪圈现象在现实中广泛存在
(1)、分部积分怪圈
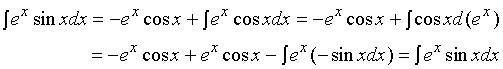
(2)、罗必达法则怪圈

(3)、图形怪圈

(4)、语义怪圈
理发师:我要为世界上所有不自已刮胡子的人刮胡子,
但不为世界上所有自己刮胡子的人刮胡子。
某 人:请问,你为自己刮胡子吗?
实际解题中,往往是第一、第二换元法与分部积分法揉合在一起使用;而且在分部积分法使用熟练之后,不必设出![]() 与
与![]() ,只要记在心中即可。
,只要记在心中即可。
【例4】求
![]()
解:令
![]() ,
, ![]() ,
, ![]()
